Hey there. I am working on the Astrometry project from Gnuastro and I will explain below the first things that I have been doing.

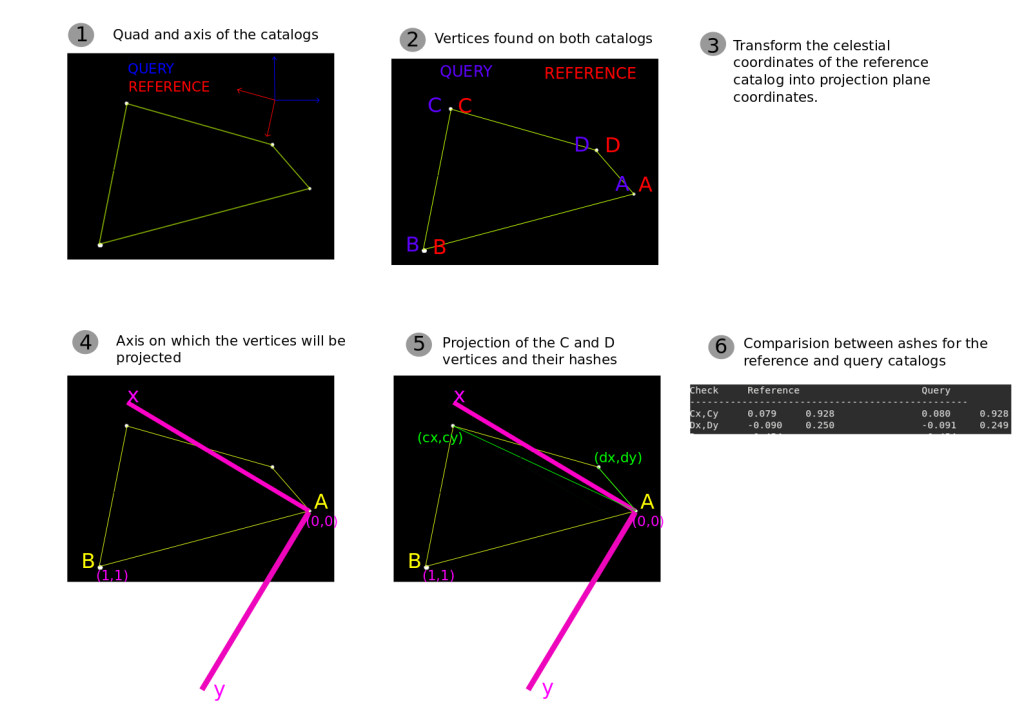
Basically, we have two catalogs: one is the query catalog, which we want to find its wcs, and the reference catalog, that gives some stars positions in celestial coordinates. We begin finding “quads”, a group of 4 stars, on both catalogs. This part was already done, but the matching part between the quads needed some fixes.

The first thing we needed to fix was the vertices found on each catalog. It’s very important that all the vertices are labeled the same. First, we label the A and B vertices as the most separated ones. In the query catalog it’s just the Euclidean distance between the points, but on the reference catalog we have to use the angular distance between the points to get the same vertices. Prior to that, it was also using the Euclidean distance to the vertices on the reference catalog, so it would give different most separated A and B for the two catalogs.
After that, we have to choose the C and D vertices. First we label randomly the two remaining vertices as C and D and then we compare the ACB and ADB angles that are less than 180 degrees and choose C to be the one that has the lesser angle.

Now, we have the A, B, C and D vertices to be the same when dealing with the same quads and we have to compute their hashes. The hashes were calculated using Cx = (c1-a1)/(b1-a1), where a1, b1 and c1 are the coordinates along the axis 1. Now we have the problem related to the rotations: the distance between the points is the same, but the distance along each axis is not the same! So the Cx would be different for different axis. The same would happen for Cy, Dx and Dy.

To solve this, first we transform the celestial coordinates of the reference catalog into projection plane coordinates (TAN projection) using the midpoint of AB as the coordinates of the native pole.
We proceed defining new two axis (x and y, where the hashes will be calculated) using the A-B vector as a 45 degrees line contained in these axis. Then, we project the C-A and D-A vectors in these axis and get the hashes.

The image below show an overview of the steps explained above.