I know I’m a bit late with this update, but I’ve been deep in the process of making everything work. The pieces we’ve been putting together since the beginning of the project are finally falling into place.

Since my last blog post, I resolved the broken data flow during the parsing of the states file. Now, all the necessary data flows cleanly through to the spectrum calculation step.

I also began getting some calculated values but something was off. Instead of showing normalized populations per electronic state, it was printing partition function values. Once corrected, the values made sense and were properly normalized.

Debug outputs:
Electronic Population Fractions:

State: A²Σ⁺ | Fraction: 0.094942 (9.49%)
State: X²Π | Fraction: 0.905058 (90.51%)

Rovibrational Population Normalization:

X²Π state: 932 rovibrational levels, sum = 1.0000000000000002
A²Σ⁺ state: 481 rovibrational levels, sum = 0.9999999999999999

Population Products (elec. fraction × rovib. sum):

State: A²Σ⁺ | Product: 0.094942
State: X²Π | Product: 0.905058
Total Sum of Products: 1.0

Next, I compared the generated spectrum with the reference one Nicolas had shared. It matched quite well except my plot showed too much population in the high vibrational states.

The root cause turned out to be the default fallback values for vibrational quantum number (v) and degeneracy when parsing failed. That’s now fixed; the correct vibrational levels are being parsed properly.

At this point, the code returns NaN for transitions with v>10, so the output is restricted to those with v≤10. In this case, 714 transitions are excluded, and the resulting spectrum closely matches the reference.

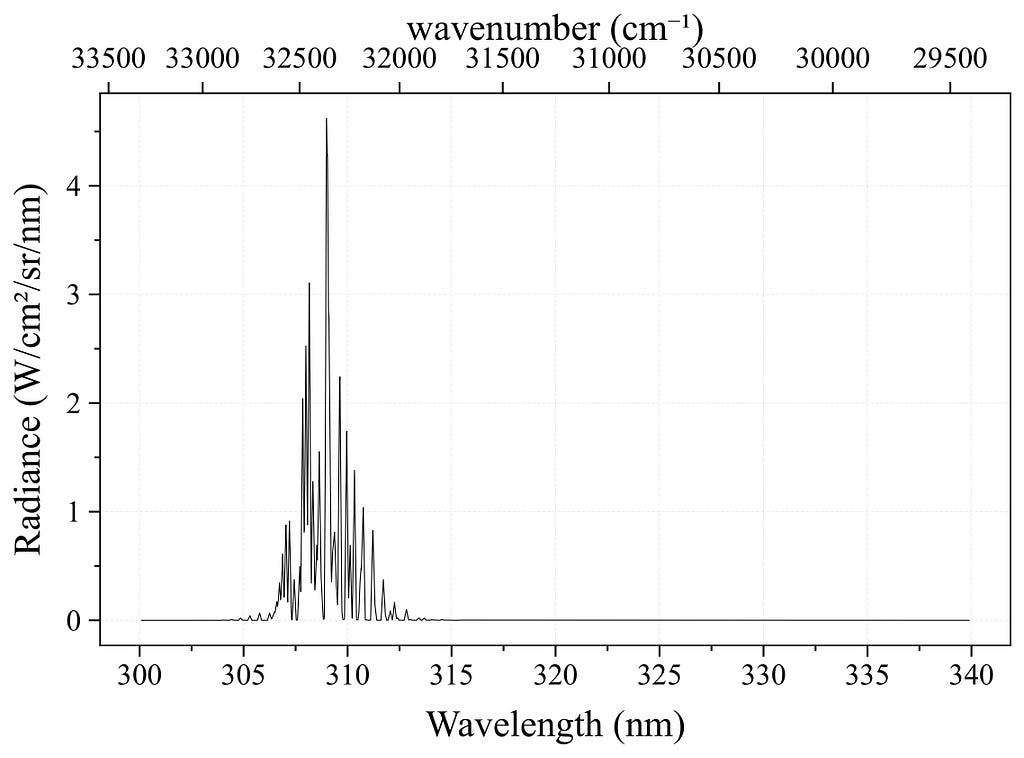
What’s causing the NaNs?
The partition function was only being calculated up to vibrational level 10, while the line database includes levels like v = 11–13. When the code attempts to fetch partition function values for these higher levels, it receives None, which becomes NaN in the DataFrame. This breaks the nu (upper state population) calculation, which relies on a valid Qrotu.

The vibrational quantum numbers in the partition function are generated in build_energy_levels_class1 using:

ElecState.Erovib(v, J=0, remove_ZPE=True)

This method:

Starts at v = 0
Increments by 1
Computes energy from spectroscopic constants
Stops when energy exceeds the dissociation limit
Generates all levels up to that point

This logic was already used for CO and CO₂ earlier in the codebase. I’m now awaiting feedback from mentors on whether we should sum the partition function only up to the dissociation limit or extend it to match all states available in the transition file.

The next step, as suggested by Nicolas, is to generalize the implementation to support any molecule from ExoMol. We can then test it by comparing with CH(A–X), which is already available in our in-house code. I’ll also clean up some redundant code that was introduced while experimenting with different approaches.