With the end of the GSoC project, I will give this blog to summarise the JAX based optimization to analyze its applicability to enhance the loglikelihood calculation. The goal is to analyze, (i) the performance of different optimizers to evaluate the loglikelihood function, (ii) demonstrated the robustness of JAX to calculate gradients. And talk about the current code and corresponding improvement due to JAX.

The application of loglikelihood fitting to periodograms is discussed in [1]. Let us start with analyzing best-fit power spectrum (i) with different sets of optimizers namely: minimize(method=’Nelder-Mead’, ’Powell’, ’CG’, ’BFGS’, ’Newton-CG’, ’L-BFGS-B’, ’TNC’, ’COBYLA’, ’SLSQP’, ’trust-constr’, ’dogleg’, ’trust-ncg’, ’trust-krylov’, ’trust-exact’). The problem setting shifts the start and test parameters to study the graph of best fit optimizer using different “methods” listed above. First, we will stick with the Powell optimizer and try to check what is the current sensitivity of the implementation.

Currently, we seek to find a solution to the problem when the optimization algorithm often gets stuck in local minima, terminate without meeting its formal success criteria, or fails due to any contributing factor. Possible ways are: (1) add more Lorentzian components, (2) reduce the amplitude, (3) start the optimization process with parameters very far away from the true parameters, (4) experiment with the different optimizers/ “methods” to investigate if there is more superior algorithm compared to Powell.

So far the Powell and Nelder-Mead gives almost the same best-fit curve compared to other optimizers, surprisingly even better than BFGS(which is a well-known numerical optimizer for an iterative method for solving unconstrained nonlinear optimization problems. This directs to more investigation with (1) and (2) and (3). Both (2) and (3) makes the algorithm fail with the current scipy.optimize.minimize, and we can see the graph as given below.

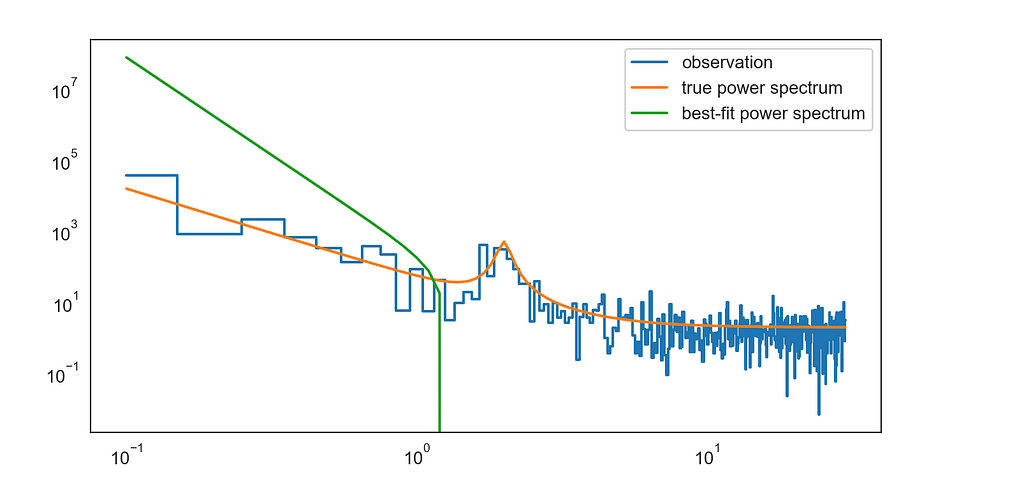
I am still holding on to try jax.scipy.optimize.minimize instead of scipy.optimize.minimize and analyze the increment in robustness. Another way to enhance the current algorithm alongside experimenting with different optimisers is:

Use a different gradient finding method.
Speed up objective function.
Reduce the number of design variables.
Choose a better initial guess.
Use parallel processing.

In my next blog, I will provide a more detailed explanation of current events. In this blog, I highlighted the emphasis of analysis.

References:

[1] Maximum likelihood fitting of X-ray power density spectra: Application to high-frequency quasi-periodic oscillations from the neutron star X-ray binary 4U1608-522. Didier Barret, Simon Vaughan. https://arxiv.org/abs/1112.0535