Images and Coordinates in Astronomy
In this lesson we are going to look at aspects of processing and viewing images specific to Astronomy and Solar Astronomy. By the end of this lesson you should understand:
- Projected Coordinate Systems in Images
- World Coordinate Systems
- Using WCS to calculate coordinates in images
- Plotting images with WCS in images
- Using SunPy Map
Projected Coordinate Systems
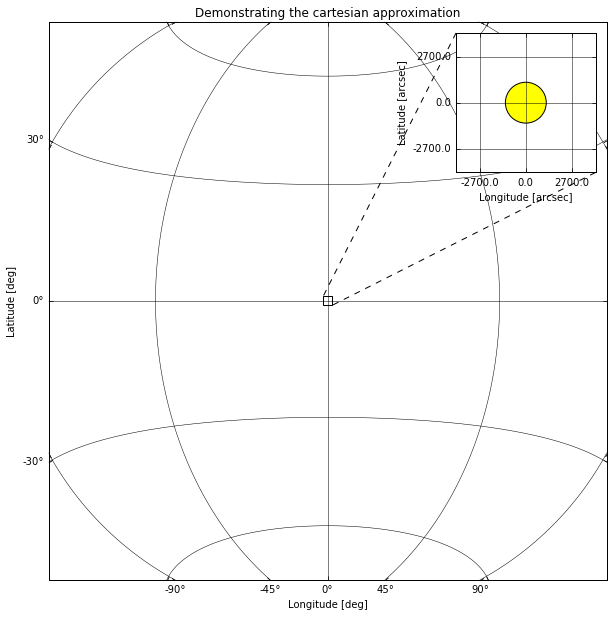
When taking images of the sky, we are projecting the spherical celestial coordinate system onto a 2-dimensional plane, which means that there is no simple linear relation between pixel coordinates and celestial coordinates
There are multiple coordinate systems used to describe the locations in 2D and 3D space for both Astronomy and Solar Physics. We shall use a couple of these systems here as examples but if you want to know more about them there are many of resources avalible.
Physical Coordinate Systems
Projected coordinate systems are one type of physical coordinate systems, they are the one we will be focusing on in this lesson due to their applicability to imaging data. Astropy and SunPy support representing point in many different physical coordinate systems, both projected and fully 3D, such as ICRS or Helioprojective.
import astropy.units as u
import sunpy.coordinates
from astropy.coordinates import SkyCoord
icrs = SkyCoord(10*u.deg, 86*u.deg, frame='icrs')
icrs
<SkyCoord (ICRS): (ra, dec) in deg
(10., 86.)>
hpc = SkyCoord(100*u.arcsec, 700*u.arcsec, obstime="now", frame='helioprojective')
hpc
<SkyCoord (Helioprojective: obstime=2018-09-06 18:18:18.345940, rsun=695508.0 km, observer=<HeliographicStonyhurst Coordinate (obstime=2018-09-06 18:18:18.345940): (lon, lat, radius) in (deg, deg, AU)
(0., 7.24812956, 1.00794235)>): (Tx, Ty) in arcsec
(100., 700.)>
hpc.transform_to('heliographic_stonyhurst')
<SkyCoord (HeliographicStonyhurst: obstime=2018-09-06 18:18:18.345940): (lon, lat, radius) in (deg, deg, km)
(10.35085155, 54.32592721, 695508.00000132)>
hpc.transform_to("icrs")
<SkyCoord (ICRS): (ra, dec, distance) in (deg, deg, km)
(56.14835134, 44.35426695, 1228805.25204128)>
World Coordinate System
From pixels to physical coordinates
The FITS files have a standard for describing the physical coordinate system associated with imaging data, this is called the world coordinate system or WCS, sometimes the specific FITS version of this is referred to as FITS-WCS.
There are multiple papers describing the FITS-WCS standard for various types of data, there is a list here: http://fits.gsfc.nasa.gov/fits_wcs.html
As you learned in the previous lesson we can load FITS files with Astropy. To demonstrate a simple example of a FITS file with FITS-WCS information in the header we shall use an image from SunPy:
from sunpy.data.sample import AIA_171_IMAGE
from astropy.io import fits
hdulist = fits.open(AIA_171_IMAGE)
hdulist.verify('silentfix')
hdulist[0].header
SIMPLE = T / conforms to FITS standard
BITPIX = -32 / array data type
NAXIS = 2 / number of array dimensions
NAXIS1 = 1024
NAXIS2 = 1024
BLD_VERS= 'V5R12X '
LVL_NUM = 1.5
T_REC = '2011-06-07T06:33:03Z'
TRECSTEP= 1.0
TRECEPOC= '1977.01.01_00:00:00_TAI'
TRECROUN= 1
ORIGIN = 'SDO '
DATE = '2012-10-16T19:45:34'
TELESCOP= 'SDO '
INSTRUME= 'AIA_3 '
DATE-OBS= '2011-06-07T06:33:02.77'
T_OBS = '2011-06-07T06:33:02.88Z'
CAMERA = 3
IMG_TYPE= 'LIGHT '
EXPTIME = 0.234256
EXPSDEV = 0.000135
INT_TIME= 0.507812
WAVELNTH= 171
WAVEUNIT= 'angstrom'
WAVE_STR= '171_THIN'
FSN = 27194331
FID = 0
QUALLEV0= 0
QUALITY = 0
TOTVALS = 16777216
DATAVALS= 16777216
MISSVALS= 0
PERCENTD= 100.0
DATAMIN = -8
DATAMAX = 17722
DATAMEDN= 18
DATAMEAN= 26.6888
DATARMS = 9429260.0
DATASKEW= 81.43300000000001
DATAKURT= 17076.7421875
DATACENT= 30.76
DATAP01 = -1.0
DATAP10 = 1.0
DATAP25 = 3.0
DATAP75 = 39.0
DATAP90 = 64.0
DATAP95 = 87.0
DATAP98 = 127.0
DATAP99 = 168.0
NSATPIX = 29
OSCNMEAN= 'nan '
OSCNRMS = 'nan '
FLAT_REC= 'aia.flatfield[:#30]'
NSPIKES = 977
CTYPE1 = 'HPLN-TAN'
CUNIT1 = 'arcsec '
CRVAL1 = 3.223099507700556
CDELT1 = 2.402792
CRPIX1 = 512.5
CTYPE2 = 'HPLT-TAN'
CUNIT2 = 'arcsec '
CRVAL2 = 1.385781353025793
CDELT2 = 2.402792
CRPIX2 = 512.5
CROTA2 = -0.138829
R_SUN = 1573.89688496
MPO_REC = 'sdo.master_pointing[:#394]'
INST_ROT= 0.019327
IMSCL_MP= 0.599489
X0_MP = 2049.459961
Y0_MP = 2049.030029
ASD_REC = 'sdo.lev0_asd_0004[:#10672125]'
SAT_Y0 = -4.519384
SAT_Z0 = 13.793308
SAT_ROT = -3.4E-05
ACS_MODE= 'SCIENCE '
ACS_ECLP= 'NO '
ACS_SUNP= 'YES '
ACS_SAFE= 'NO '
ACS_CGT = 'GT3 '
ORB_REC = 'sdo.fds_orbit_vectors[2011.06.07_06:33:00_UTC]'
DSUN_REF= 149597870691.0
DSUN_OBS= 151846026489.0
RSUN_REF= 696000000.0
RSUN_OBS= 945.4367109999999
GAEX_OBS= -13315441.72
GAEY_OBS= -25080995.82
GAEZ_OBS= 31173320.91
HAEX_OBS= -36634444009.2
HAEY_OBS= -147360551017.0
HAEZ_OBS= 35731768.47
OBS_VR = 86.97246699999999
OBS_VW = 31968.269521
OBS_VN = 4842.822869
CRLN_OBS= 340.698273
CRLT_OBS= 0.048591
CAR_ROT = 2111
HGLN_OBS= 0.0
HGLT_OBS= 0.048591
ROI_NWIN= -2147483648
ROI_SUM = -2147483648
ROI_NAX1= -2147483648
ROI_NAY1= -2147483648
ROI_LLX1= -2147483648
ROI_LLY1= -2147483648
ROI_NAX2= -2147483648
ROI_NAY2= -2147483648
ROI_LLX2= -2147483648
ROI_LLY2= -2147483648
PIXLUNIT= 'DN '
DN_GAIN = 17.7
EFF_AREA= 2.419
EFF_AR_V= 3.0
TEMPCCD = -71.0
TEMPGT = 14.327
TEMPSMIR= 34.029
TEMPFPAD= 16.29
ISPSNAME= 'aia.lev0_isp_0011'
ISPPKTIM= '2011-06-07T06:32:57.50Z'
ISPPKTVN= '001.197 '
AIVNMST = 453
AIMGOTS = 1686119616
ASQHDR = 2174677979
ASQTNUM = 2
ASQFSN = 27194331
AIAHFSN = 27194323
AECDELAY= 1537
AIAECTI = 0
AIASEN = 0
AIFDBID = 241
AIMGOTSS= 55109
AIFCPS = 10
AIFTSWTH= 0
AIFRMLID= 3057
AIFTSID = 41729
AIHISMXB= 7
AIHIS192= 8377773
AIHIS348= 8384772
AIHIS604= 8386035
AIHIS860= 8386516
AIFWEN = 204
AIMGSHCE= 237
AECTYPE = 2
AECMODE = 'ON '
AISTATE = 'CLOSED '
AIAECENF= 1
AIFILTYP= 0
AIMSHOBC= 41.104
AIMSHOBE= 26.068001
AIMSHOTC= 55.327999
AIMSHOTE= 69.344002
AIMSHCBC= 275.432007
AIMSHCBE= 260.484009
AIMSHCTC= 289.556
AIMSHCTE= 303.395996
AICFGDL1= 0
AICFGDL2= 107
AICFGDL3= 171
AICFGDL4= 236
AIFOENFL= 1
AIMGFSN = 5
AIMGTYP = 0
AIAWVLEN= 7
AIAGP1 = 0
AIAGP2 = 0
AIAGP3 = 0
AIAGP4 = 0
AIAGP5 = 0
AIAGP6 = 0
AIAGP7 = 0
AIAGP8 = 619
AIAGP9 = 683
AIAGP10 = 748
AGT1SVY = 2
AGT1SVZ = -6
AGT2SVY = 0
AGT2SVZ = -1
AGT3SVY = -2
AGT3SVZ = 3
AGT4SVY = -5
AGT4SVZ = 5
AIMGSHEN= 4
KEYWDDOC= 'https: '
RECNUM = 76618218
BLANK = -32768
DATE_OBS= '2011-06-07T06:33:02.77'
XCEN = 2.91938326953
YCEN = 1.09323792231
DETECTOR= 'AIA '
COMMENT FITS (Flexible Image Transport System) format is defined in 'Astronomyan
COMMENT d Astrophysics', volume 376, page 359; bibcode: 2001A&A...376..359HFITSH
COMMENT EAD2STRUCT
HISTORY FITSHEAD2STRUCT run at: Fri May 26 11:33:15 2017mreadfits_shm VERSION:
HISTORY 1.20read_sdo VERSION: 2.10aia2wcsmin.pro VERSION: 5.10aia2wcsminaia2wc
HISTORY smin MPO_date: 2012-09-04T00:00:00Zaia2wcsmin MPO_t_start: 2011-06-05T
HISTORY 00:00:00Zaia2wcsmin MPO_t_stop: 2011-06-12T00:00:00Zaia2wcsmin MPO_ver
HISTORY sion: 5ssw_reg.pro VERSION: 1.30ssw_regssw_reg ROT called with cubic i
HISTORY nterpolation: cubic = -0.500000ssw_reg Image registered to SDO image wi
HISTORY th FSN = 27194330ssw_reg Image registered to SDO image with T_OBS = 201
HISTORY 1-06-07T06:33:01.aia_fix_header.pro VERSION: 1.00aia_prep.pro VERSION:
HISTORY 5.10aia_reg.pro VERSION: 1.20
As you can see there are lots of keys in this and most other real world FITS headers. The ones we need to understand for FITS-WCS are:
Reference Pixel and Coordinate:
header = hdulist[0].header
print(header['CRVAL1'], header['CRVAL2'])
print(header['CRPIX1'], header['CRPIX2'])
3.223099507700556 1.385781353025793
512.5 512.5
Pixel resolution (at the reference pixel):
print(header['CDELT1'], header['CDELT2'])
2.402792 2.402792
Rotation angle, in degress (at the reference pixel):
print(header['CROTA2'])
-0.138829
Coordinate System and Projection:
print(header['CTYPE1'], header['CTYPE2'])
HPLN-TAN HPLT-TAN
Keyword Extraction
Extract and print out the TELESCOP value from the header.
Next, extract the WAVELNTH and WAVEUNIT values, use these to construct an astropy Quantity object for the wavelength of this image.
Solution
header['TELESCOP']
'SDO'
import astropy.units as u
u.Quantity(header['WAVELNTH'], unit=header['WAVEUNIT'])
$171 \; \mathrm{\mathring{A}}$
We could now sit down and work out how to convert from a pixel coordinate to a physical coordinate described by this header (Helioprojective).
However, we can cheat and just use Astropy.
from astropy.wcs import WCS
wcs = WCS(header)
wcs
WCS Keywords
Number of WCS axes: 2
CTYPE : 'HPLN-TAN' 'HPLT-TAN'
CRVAL : 0.00089530541880571 0.00038493926472938695
CRPIX : 512.5 512.5
NAXIS : 1024 1024
We can convert from pixel to world coordinate:
wcs.wcs_pix2world(((100, 100),), 0)
array([[ 3.59725580e+02, -2.73595993e-01]])
Or back again:
wcs.wcs_world2pix([[ 3.59725669e+02, -2.74328093e-01]], 0)
array([[100.13559125, 98.90341705]])
The last parameter to the two above examples is the ‘origin’ parameter. It is a flag that tells WCS if you indexes should be 0-based (like numpy) or 1-based (like FITS). Here we are using 0 as we want to convert to and from numpy indexes of the array.
Where are my Pixels?
[-500, 0]
[500, 500]
[0, 0]
Solution
print(wcs.wcs_pix2world(((-500, 0),), 1))
print(wcs.wcs_pix2world(((500, 500),), 1))
print(wcs.wcs_pix2world(((0, 0),), 1))
[[ 3.59324315e+02 -3.40013041e-01]]
[[ 3.59992532e+02 -7.93784855e-03]]
[[ 3.59658007e+02 -3.40839229e-01]]
WCS and SkyCoord
A common usecase for WCS + Coordinates is to store or transform from pixel coordinates to one or more different physical coordinates. Combining Astropy WCS and Coordinates makes this easy.
Assuming we have the WCS object we created from the FITS header above we can get an astropy Coordinate Frame:
from astropy.wcs.utils import wcs_to_celestial_frame
hpc_frame = wcs_to_celestial_frame(wcs)
hpc_frame
<Helioprojective Frame (obstime=2011-06-07 06:33:02.770000, rsun=695508.0 km, observer=earth)>
We can then use this when creating SkyCoord objects:
SkyCoord(100*u.arcsec, -500*u.arcsec, frame=hpc_frame)
<SkyCoord (Helioprojective: obstime=2011-06-07 06:33:02.770000, rsun=695508.0 km, observer=<HeliographicStonyhurst Coordinate (obstime=2011-06-07 06:33:02.770000): (lon, lat, radius) in (deg, deg, AU)
(0., 0.03652003, 1.01484379)>): (Tx, Ty) in arcsec
(100., -500.)>
Note: For solar data you should always use sunpy.map for this
Coordinate Aware Plotting
In this section we are going to use the astropy.visualization.wcsaxes subpackage to make WCS aware image plots.
For this example we are going to use a Hubble image.
from astropy.io import fits
hdulist = fits.open('h_n4571_f555_mosaic.fits.gz')
hdulist
[<astropy.io.fits.hdu.image.PrimaryHDU object at 0x7f418f44a7b8>]
wcs = WCS(hdulist[0].header)
import matplotlib.pyplot as plt
ax = plt.subplot(111, projection=wcs)
ax.imshow(hdulist[0].data, cmap='gray', vmax=1000, interpolation=None, origin='lower')
<matplotlib.image.AxesImage at 0x7f418d2f58d0>

This image now has physcial labels in the native coordinate system of the image. We can see what the coordinate system and projection of this image is using the ‘CTYPE’ header entries we saw earlier.
print(hdulist[0].header['CTYPE1'], hdulist[0].header['CTYPE2'])
RA---TAN DEC--TAN
We can tell that this is in the FK5 coordinate system by the presence of a ‘equinox’ entry in the header:
hdulist[0].header['equinox']
2000.0
Add some labels
Now we have a nice plot with physically meaningful ticks, we should label our axes.
Add labels to the axes saying "Right Ascension [degrees]" and "Declination [degrees]"
Also overlay a coordinate grid using:
ax.coords.grid()
Look up the documentation for this method to see what parameters you can specify.
Solution
plt.figure()
ax = plt.subplot(111, projection=wcs)
ax.imshow(hdulist[0].data, cmap='gray', vmax=1000, interpolation=None, origin='lower')
ax.set_xlabel("Right Ascension [degrees]")
ax.set_ylabel("Declination [degrees]")
ax.coords.grid(color='white', alpha=0.5, linestyle='solid')

Now we have a nice plot, we can do a couple of things to plot.
Overplotting in Pixel Coordinates
plt.figure()
ax = plt.subplot(111, projection=wcs)
ax.imshow(hdulist[0].data, cmap='gray', vmax=1000, interpolation=None, origin='lower')
ax.set_xlabel("Right Ascension [degrees]")
ax.set_ylabel("Declination [degrees]")
ax.coords.grid(color='white', alpha=0.5, linestyle='solid')
ax.plot(3000, 3000, 'o')
[<matplotlib.lines.Line2D at 0x7f4184acb4a8>]

Overplotting in World Coordinates
fig = plt.figure()
ax = plt.subplot(111, projection=wcs)
ax.imshow(hdulist[0].data, cmap='gray', vmax=1000, interpolation=None, origin='lower')
ax.set_xlabel("Right Ascension [degrees]")
ax.set_ylabel("Declination [degrees]")
ax.coords.grid(color='white', alpha=0.5, linestyle='solid')
ax.set_autoscale_on(False)
ax.plot(3000, 3000, 'o')
# Overplot in FK5
ax.plot_coord(SkyCoord(189.25*u.deg, 14.23*u.deg, frame="fk5"), "o")
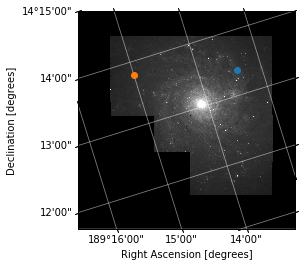
Overplot in a different coordinate system
Using ax.get_transform() you can specify coordinates in any system that astropy coordinates can transform to, try overplotting a point in the 'galactic' system.
Also overlay a coordinate grid using:
ax.coords.grid()
Look up the documentation for this method to see what parameters you can specify.
Overplotting Another Coordinate System
fig = plt.figure()
ax = plt.subplot(111, projection=wcs)
ax.imshow(hdulist[0].data, cmap='gray', vmax=1000, interpolation=None, origin='lower')
ax.set_xlabel("Right Ascension [degrees]")
ax.set_ylabel("Declination [degrees]")
ax.coords.grid(color='white', alpha=0.5, linestyle='solid')
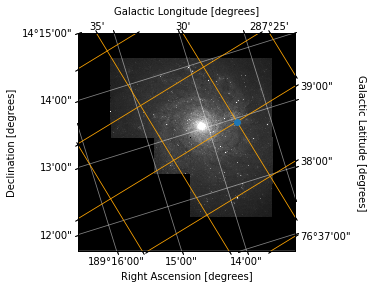
overlay = ax.get_coords_overlay('galactic')
overlay.grid(color='orange', alpha=1, linestyle='solid')
overlay['l'].set_axislabel("Galactic Longitude [degrees]")
overlay['b'].set_axislabel("Galactic Latitude [degrees]")
ax.plot_coord(SkyCoord(287.5*u.deg, 76.65*u.deg, frame="galactic"), "o")
SunPy Map
The SunPy Map class is a wrapper for solar images which makes some of the above opertations easier.
import sunpy.map
from sunpy.data.sample import AIA_171_ROLL_IMAGE
amap = sunpy.map.Map(AIA_171_ROLL_IMAGE)
amap.peek()

Coordinate Systems
The SunPy map will calculate some of the things we did earlier automatically, and add some extra information.
amap.coordinate_system
SpatialPair(axis1='HPLN-TAN', axis2='HPLT-TAN')
amap.coordinate_frame
<Helioprojective Frame (obstime=2014-04-09 06:00:12.970000, rsun=696000000.0 m, observer=<HeliographicStonyhurst Coordinate (obstime=2014-04-09 06:00:12.970000): (lon, lat, radius) in (deg, deg, m)
(0., -6.047074, 1.49860274e+11)>)>
amap.wcs
WCS Keywords
Number of WCS axes: 2
CTYPE : 'HPLN-TAN' 'HPLT-TAN'
CRVAL : 0.0 0.0
CRPIX : 2053.459961 2047.880005
PC1_1 PC1_2 : 0.7073447192241196 0.7068687630570128
PC2_1 PC2_2 : -0.7068687630570128 0.7073447192241196
CDELT : 0.599489 0.599489
NAXIS : 0 0
Plotting
SunPy map uses these attributes to do it’s plotting with WCSAxes like we did manually earlier. We can therefore use the overplotting and grid techniques to improve the plot:
import astropy.units as u
fig = plt.figure()
amap = sunpy.map.Map(AIA_171_ROLL_IMAGE)
im = amap.plot()
ax = plt.gca()
x = 500*u.arcsec
y = -300*u.arcsec
ax.plot_coord(SkyCoord(x, y, frame=amap.coordinate_frame), "o")
overlay = ax.get_coords_overlay('heliographic_stonyhurst')
overlay.grid(color='cyan', alpha=1, linestyle='solid')

amap.pixel_to_data(100*u.pix, 200*u.pix)
<SkyCoord (Helioprojective: obstime=2014-04-09 06:00:12.970000, rsun=696000000.0 m, observer=<HeliographicStonyhurst Coordinate (obstime=2014-04-09 06:00:12.970000): (lon, lat, radius) in (deg, deg, m)
(0., -6.047074, 1.49860274e+11)>): (Tx, Ty) in arcsec
(-1610.53285218, 44.2122476)>
amap.data_to_pixel(SkyCoord(0*u.arcsec, 0*u.arcsec, frame=amap.coordinate_frame))
PixelPair(x=<Quantity 2052.459961 pix>, y=<Quantity 2046.880005 pix>)
Rotate your Owl
Why is the Sun wonky?
Use the rotate() method of SunPy Map to align the coordinate grid to the pixel grid in this sample image.
Once you have run rotate, plot the resulting image, and compare with the one above.
mr = amap.rotate()
mr.peek()
---------------------------------------------------------------------------
MemoryError Traceback (most recent call last)
<ipython-input-43-194907119f42> in <module>()
----> 1 mr = amap.rotate()
2 mr.peek()
/opt/miniconda/envs/stfc/lib/python3.6/site-packages/sunpy/map/mapbase.py in rotate(self, angle, rmatrix, order, scale, recenter, missing, use_scipy)
1150 image_center=np.flipud(pixel_center),
1151 recenter=recenter, missing=missing,
-> 1152 use_scipy=use_scipy).T
1153
1154 if recenter:
/opt/miniconda/envs/stfc/lib/python3.6/site-packages/sunpy/image/transform.py in affine_transform(image, rmatrix, order, scale, image_center, recenter, missing, use_scipy)
130
131 rotated_image = skimage.transform.warp(adjusted_image, tform, order=order,
--> 132 mode='constant', cval=missing)
133
134 return rotated_image
/opt/miniconda/envs/stfc/lib/python3.6/site-packages/skimage/transform/_warps.py in warp(image, inverse_map, map_args, output_shape, order, mode, cval, clip, preserve_range)
883 input_shape[2])
884
--> 885 coords = warp_coords(coord_map, output_shape)
886
887 # Pre-filtering not necessary for order 0, 1 interpolation
/opt/miniconda/envs/stfc/lib/python3.6/site-packages/skimage/transform/_warps.py in warp_coords(coord_map, shape, dtype)
596 # Map each (row, col) pair to the source image according to
597 # the user-provided mapping
--> 598 tf_coords = coord_map(tf_coords)
599
600 # Reshape back to a (2, M, N) coordinate grid
/opt/miniconda/envs/stfc/lib/python3.6/site-packages/skimage/transform/_warps.py in coord_map(*args)
874
875 def coord_map(*args):
--> 876 return inverse_map(*args, **map_args)
877
878 if len(input_shape) == 3 and len(output_shape) == 2:
/opt/miniconda/envs/stfc/lib/python3.6/site-packages/skimage/transform/_geometric.py in __call__(self, coords)
571
572 """
--> 573 return self._apply_mat(coords, self.params)
574
575 def inverse(self, coords):
/opt/miniconda/envs/stfc/lib/python3.6/site-packages/skimage/transform/_geometric.py in _apply_mat(self, coords, matrix)
548
549 x, y = np.transpose(coords)
--> 550 src = np.vstack((x, y, np.ones_like(x)))
551 dst = np.dot(src.transpose(), matrix.transpose())
552
/opt/miniconda/envs/stfc/lib/python3.6/site-packages/numpy/core/shape_base.py in vstack(tup)
232
233 """
--> 234 return _nx.concatenate([atleast_2d(_m) for _m in tup], 0)
235
236 def hstack(tup):
MemoryError: